Process Capability & Performance (III)

Muy estimados lectores, nos encontramos ya en la tercera y última parte de este complejo tema que nos concierne: el análisis de la Capacidad y Desempeño de nuestros procesos.

Recordemos que en la segunda entrega nos detuvimos en las siguientes definiciones fundamentales:

• PP: significa "Process Performance" y nos indica el Desempeño Potencial de nuestro proceso.

• PPK también significa "Process Performance", pero nos indica el Desempeño Real de nuestro proceso.

• PPL significa "Process Performance to Lower Limit" y mide qué tan cerca la media del proceso se encuentra del límite inferior.

• PPU significa "Process Performance to Upper Limit" y mide qué tan cerca la media del proceso se encuentra del límite superior.

• PP y PPK son indicadores de largo plazo.

• CP significa "Capability Process" y mide la Capacidad Potencial del proceso.

• CPK también significa "Capability Process", pero nos indica la Capacidad Real del proceso.

• CP y CPK son parámetros de corto plazo.

Una vez que tenemos los datos y verificamos que se corresponden con una distribución normalizada, o que, si no lo es, la hemos normalizado, procederemos a calcular los PP y CP. Es importante recordar que los CP y CPK solo se pueden calcular si hemos tomado datos en subgrupos. Por ejemplo, si tomamos 30 datos de cada campaña de fabricación y llevamos a cabo 4 campañas en el año, tendríamos 4 subgrupos de 30 datos cada uno.

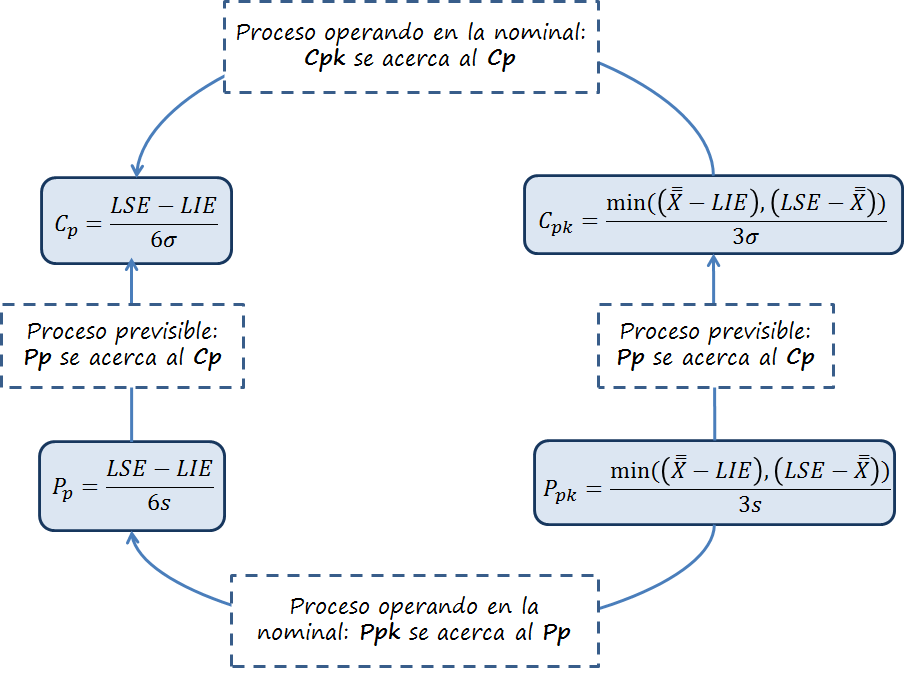
¿Cuáles son las fórmulas a aplicar? Pues las siguientes:

 

 

...donde:

• USL es el Límite Superior de la Especificación.

• LSL es el Límite Inferior de la Especificación.

• Sigma within es veces la desviación estándar dentro de cada subgrupo.

• Sigma overall es la desviación estándar total de todos los subgrupos considerados como uno solo.

 

 

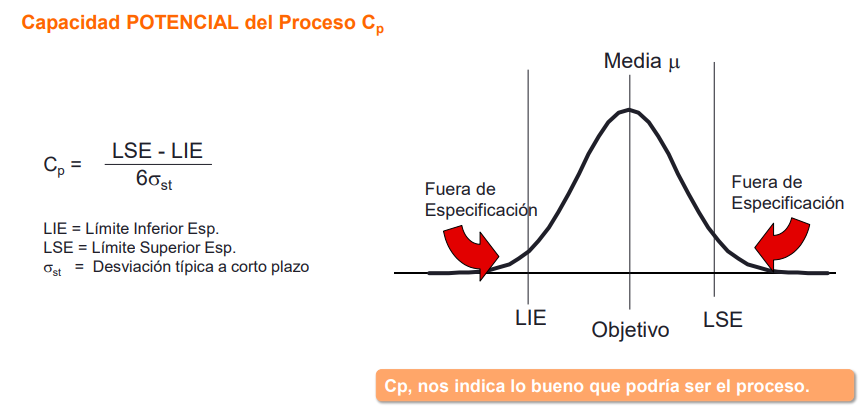
El CPK es el valor mínimo cual sea del CPU o de CPL

El PPK es el valor mínimo cual sea del PPU o de PPL

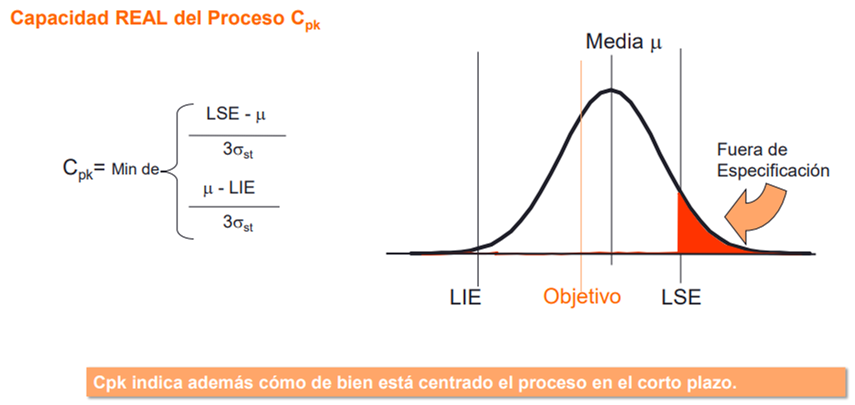
Ya sabemos todos cómo se calcula la desviación estándar overall, que es la desviación estándar tradicional, cuya fórmula la tenemos en nuestro primer artículo; pero..., ¿y cómo se calcula la desviación within? Fácil..., cuya fórmula es muy sencilla y es la siguiente:

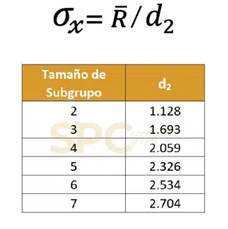
La desviación estándar en CP/CPK (Within) es el rango promedio de una constante, d2, cuyo valor está tabulado y depende del grupo y del subgrupo. El Rango Promedio (R?) es la media de los rangos (valor mayor menos rango menor). Utilizaremos la siguiente tabla:

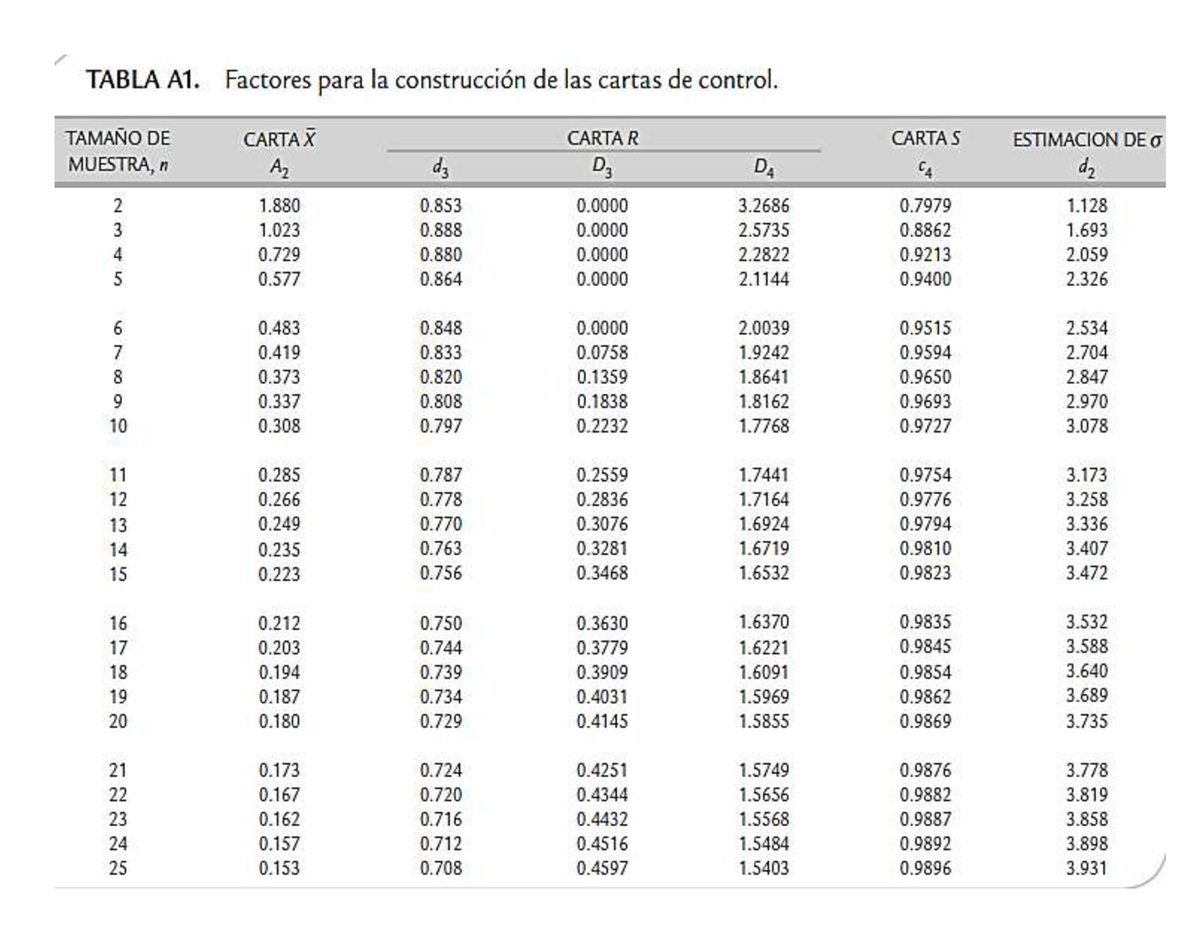
Es decir, tomamos el valor mayor, le restamos el rango menor, y utilizamos la estimación de d2 de la tabla correspondiente al número de subgrupos que tenemos, en la columna de Tamaño de Muestra, n, aplicando la fórmula para obtener la desviación within.

No obstante, estimados lectores, para vuestra tranquilidad, todo esto lo calcula automáticamente el maravilloso Minitab. Sin embargo, como decía un profesor mío de matemáticas, es importante entender la esencia de las fórmulas, y creo que tenía razón.

Como veréis, las fórmulas para calcular los PP, PPK, CP y CPK son idénticas; solo se diferencian en la desviación estándar que se utiliza en dichas fórmulas, aspecto crucial. Y recordad, es fundamental tener subgrupos para calcular correctamente los CP.

Estamos llegando al final...

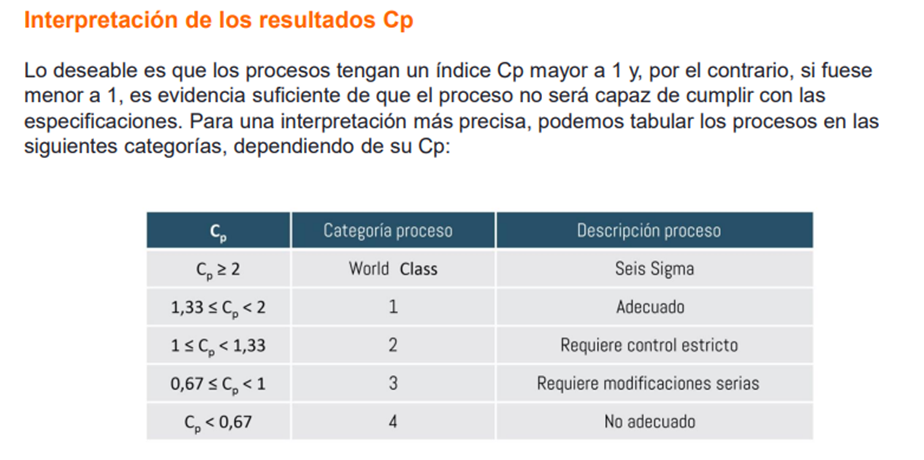
Ahora, una vez que hemos obtenido los valores para nuestros cuatro parámetros principales, debemos interpretar qué significan en cuanto al estado de nuestro proceso. Aunque existen diferentes interpretaciones, indicaré la más frecuente y cercana al proceso de la industria farmacéutica que nos atañe. Pueden existir diferencias entre sectores, dependiendo del número de no conformidades que se esté dispuesto a asumir, pero la mayoría acepta que:

• Si los índices de CP y CPK tienen un valor mayor de 1, el proceso es capaz y existe una probabilidad baja de salirse de los valores de especificación.

• Si los índices de CP y CPK tienen un valor entre 1,33 y 2,0, el proceso es capaz y existe una probabilidad baja de salirse de los valores de especificación.

• Si los índices de CP y CPK tienen un valor menor de 1, el proceso no es capaz y existe una probabilidad alta, mayor cuanto menores sean los valores, de salirse de los valores de especificación.

• Si CP es mayor que 1 y CPK es menor de 1, el proceso es capaz, pero no está centrado. El proceso está centrado cuando CP es igual a CPK.

• Si el índice de PP tiene un valor mayor de 1, el proceso tiene una potencialidad de desempeño correcta.

• Si el índice de PPK tiene un valor mayor de 1, el proceso tiene un desempeño real correcto.

• Si los índices de PP y PPK tienen un valor entre 1,33 y 2,0, el performance potencial y real del proceso es excelente.

• Si los índices de PP y PPK tienen un valor menor de 1, aunque el proceso sea capaz, el performance real y potencial del proceso es muy bajo y existe una probabilidad alta, mayor cuanto menores sean los valores, de salirse de los valores de especificación.

Es decir, imaginemos que saltamos a pértiga y, entrenando con 30 saltos realizados, 28 de ellos han sido válidos. Somos capaces potencial y realmente (CP y CPK), pero ahora imaginemos que vamos a ejecutar el salto en las Olimpiadas y fallamos... éramos capaces, pero el performance ha sido malo (PP, PPK).

Para un mejor entendimiento, veamos y analicemos la siguiente tabla:

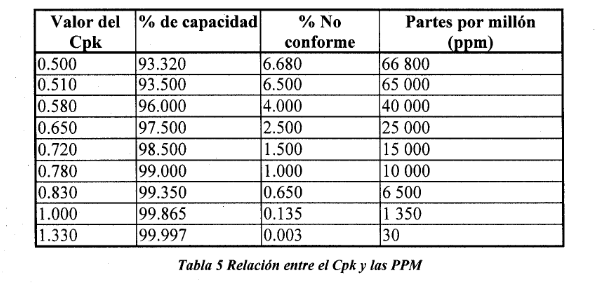
Es decir, para un valor de CPK (Capacidad Real) de 1.33, podríamos tener 30 unidades defectuosas, o 60 valores por millón, fuera de especificaciones. Si adoptamos 1 como valor, podríamos tener 1,350 por millón, o lo que es lo mismo, 1.3 por cada 1000. Por ello, como comentamos antes, cuanto más estrictos queramos ser, mayores valores de CP y PP debemos exigir a nuestros procesos.

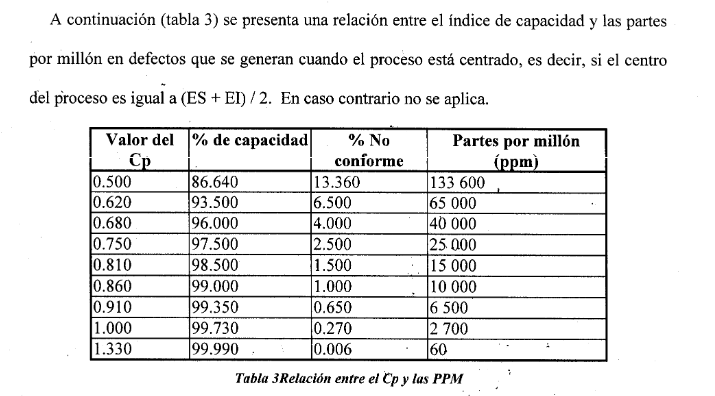
Es decir, para un valor de CP (Capacidad Potencial) de 1.33 podríamos tener 60 unidades defectuosas, o 60 valores por millón, fuera de especificaciones. Si adoptamos 1 como valor, podríamos tener 2,700 por millón, o lo que es lo mismo, 2.7 por cada 1000.

Resumiendo, debemos tener valores de CP, CPK, PP y PPK por encima de 1.33 como mínimo. Si obtenemos valores menores de 1, es necesario revisar profundamente el proceso para hacerlo capaz...

Espero que estos tres artículos hayan sido útiles y, si tenéis alguna duda, ya sabéis dónde estoy.